一个格点问题
我觉得下面的问题是有趣的:
问题 1. 试求欧氏平面上以原点为中心$R$为半径的开圆盘内有多少个形如$(m,n)$的整数点, 其中$m,n$都是整数?
我的想法是利用计算机来具体的计算有多少个格点.
首先, 我们可以用一个函数$F$来判断给定的$(m,n)$是否是满足条件的点, 明显$F$可取为
$$F(x,y,R)=x^2+y^2-R^2$$
如果, $F(m,n,R)<0$则$(m,n)$就是满足条件的一个点. 注意到$x,y$的范围为:$-R< x ,y< R$, 这样我们很容易用两个循环来计算给定$R$时, 满足要求的点有多少个.
Mathematica代码
|
1 2 3 4 5 6 |
F[x_, y_, R_] := x^2 + y^2 - R^2 Num[R_] := Length@DeleteDuplicates@Flatten[Table[ If[F[i, j, R] < 0, {{i, j}, {-i, j}, {i, -j}, {-i, -j}, {j, i}, {j, -i}, {-j, i}, {-j, -i}}, {{0, 0}} ], {i, 0, Floor[R]}, {j, i, Floor[R]}], 2] |
可以轻易用如下代码作出图形:
|
1 |
Plot[Num[x], {x, 0, 5}] |
这表示在0到5之间时, 函数的图像.
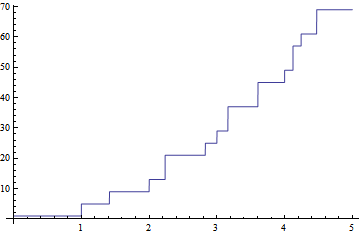
类似可得:
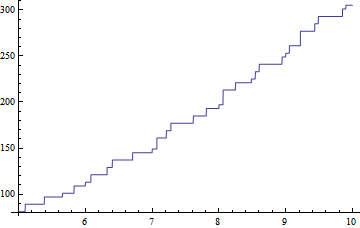
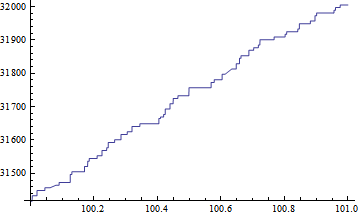
未解决的问题
- 如何找到图中的间断点?
- 如何优化代码, 当数值很大时, 计算几乎不能进行
发表回复