中考测试题
满分100分,时间2小时
- (5′) 正五边形广场ABCDE的边长为80m,甲、乙两个同学做游戏,分别从A、C两点处同时出发,沿A-B-C-D-E-A的方向绕广场行走,甲的速度为50m/min,乙的速度为46m/min,则两人第一次刚走到同一条边上时,甲在顶点( )处。
- (8′, 湖北武汉2019). 已知$AB$是圆$O$的直径,$AM$和$BN$是圆$O$的两条切线,$DC$与圆$O$相切于点$E$,分别交$AM$、$BN$于$D$、$C$两点.
(1). 求证$AB^2=4AD\cdot BC$;
(2). 连接$OE$并延长交$AM$于$F$,连接$CF$. 若$\angle ADE=2\angle OFC$,$AD=1$, 求图中阴影部分的面积.
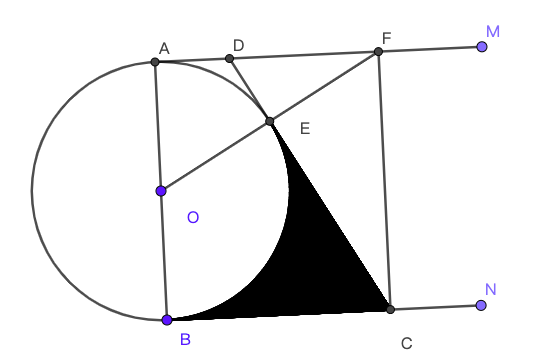
图 1. 第二题 - (14′, 广州2019) 假设等边三角形$\Delta ABC$中, $AB=6$,$D$在$BC$上,$BD=4$. 点$E$为边$AC$上一动点(不与$C$重合),三角形$\Delta CDE$关于$DE$的轴对称图形为$\Delta FDE$.
(1) 当点$F$在$AC$上时,求证: $DF//AB$;
(2) 设$\Delta ACD$的面积为$S_1$, $\Delta ABF$的面积为$S_2$, 记$S=S_1-S_2$, 问$S$是否存在最大值?若存在,求出该最大值,否则说明理由。
(3) 当$B$、$F$、$E$三点共线时,求$AE$的长。
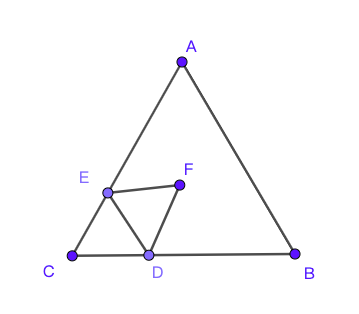
图 2. 第三题
- (10′, 湖北荆门2019)已知$ABCD$是正方形,点$E$是$AB$上的动点,作等腰直角三角形$FEC$,其中$\angle E$为直角。
(1)过$F$作$AD$的垂线,垂足为$G$。试问$FG$是否总等于$AG$? 说明理由;
(2)连接$FC$并设其中点为$H$,试问$HD=HG$是否总成立?说明理由。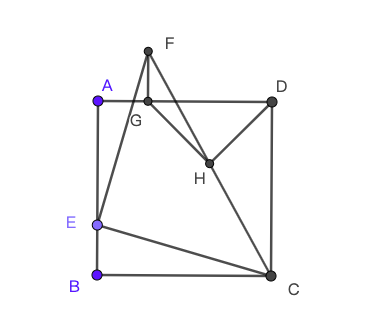
图 3. 第四题 - (12’,湖北荆门2019). 已知抛物线$y=ax^2+bx+c$顶点为$(2,-1)$且经过点$(0,3)$. 假设它与直线$y=x-1$交与点$A$、$B$.
(1) 求抛物线的解析式
(2) 若在抛物线上恰好只有三点$Q$、$M$、$N$使得$S_{\Delta QAB}=S_{\Delta MAB}=S_{\Delta NAB}=S$, 求$S$的值;
(3) 在$A$、$B$之间的抛物线弧上是否存在点$P$满足$\angle APB=90^\circ$? 若存在求出$P$的横坐标,否则请说明理由。(回忆,坐标平面内两点$M(x_1,y_1)$、$N(x_2,y_2)$之间的距离为
$\overline{MN}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$. )
图 3. 第四题 - (13′, 江苏泰安2019)若二次函数$y=ax^2+bx+c$的图像与$x$、$y$轴分别交于点$A(3,0)$、$B(0,-2)$且过点$C(2,-2)$.
(1) 求二次函数的表达式;
(2) 若点$P$为抛物线上第一象限内的点,且$S_{\Delta PBA}=4$, 求$P$的坐标;
(3) 在抛物线上($AB$下方)是否存在点$M$,使得$\angle ABO=\angle ABM$? 若存在求出$M$到$y$轴到距离,否则说明理由。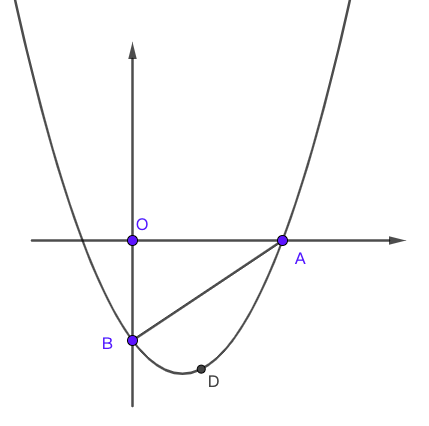
图 5. 第六题 - (14′, 广州2019)已知抛物线$G: y=mx^2-2mx-3$有最低点.
(1) 求二次函数$y=mx^2-2mx-3$的最小值(用含$m$的式子表示);
(2) 将抛物线$G$向右平移$m$个单位得到抛物线$G_1$, 经探究发现,随着$m$的变化,抛物线$G_1$的顶点之纵坐标$y$与横坐标$x$之间存在一个函数关系,试求这个函数关系式,并写出自变量$x$的取值范围。
(3) 记(2)中所求得得函数为$H$, 抛物线$G$与$H$的图像交于点$P$, 结合图像求点$P$的纵坐标的取值范围。 - (12′, 成都2019) 如图,抛物线$y=ax^2+bx+c$经过点$A(-2,5)$, 与$x$轴交于点$B(-1,0)$, $C(3,0)$.
(1) 求抛物线的函数表达式;
(2) 点$D$在抛物线的对称轴上,且位于$x$轴的上方,将$\Delta BCD$沿直线$BD$翻折得到$\Delta BC’D$, 若点$C’$恰好落在抛物线的对称轴上,求点$C’$和点$D$的坐标;
(3) 设$P$是抛物线上位于对称轴右侧的一点,点$Q$在抛物线的对称轴上,当$\Delta CPQ$为等边三角形时,求直线$BP$的函数表达式。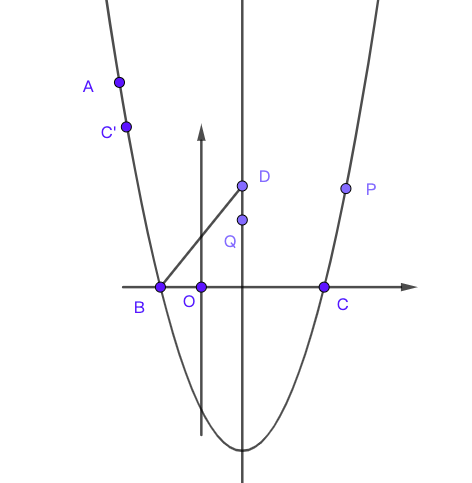
图 6. 第八题 - (12′, 武汉2019) 已知抛物线$C_1: y=(x-1)^2-4$和$C_2:y=x^2$
(1) 如何将抛物线$C_1$平移得到抛物线$C_2$ ?
(2) 如果抛物线$C_1$与$x$正半轴交于点$A$, 经过点$A$的直线$y=-\frac{4}{3} x+b$交抛物线$C_1$于另一点$B$. 试在线段$AB$上求点$P$,使得过点$P$作直线$PQ//y$轴交抛物线$C_1$于点$Q$:
(a) 若$AP=AQ$,求点$P$的横坐标;
(b) 若$PA=PQ$,直接写出点$P$的横坐标;
(3) $\Delta MNE$的顶点$M$、$N$在抛物线$C_2$上,点$M$在点$N$右边,有两条直线$ME$、$NE$于抛物线$C_2$都有唯一公共点,$ME$、$NE$均与$y$轴不平行。若三角形$\Delta MNE$的面积为2, 设$M$、$N$两点的横坐标分别为$m$、$n$,求$m$于$n$的数量关系。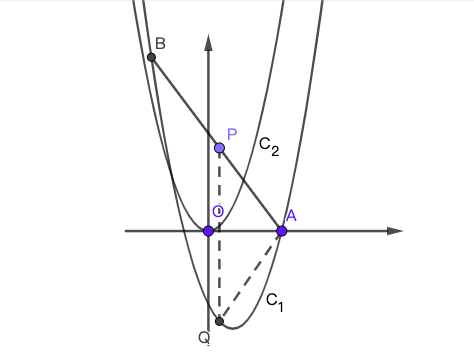
图 7. 第九题(2)(a) 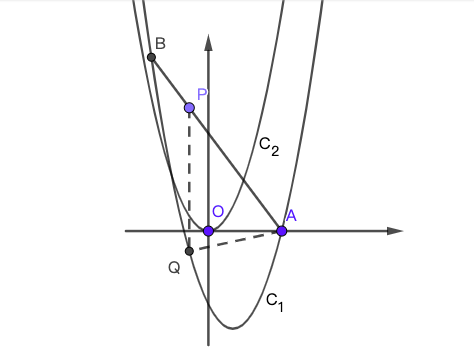
图 8. 第九题(2)(b) 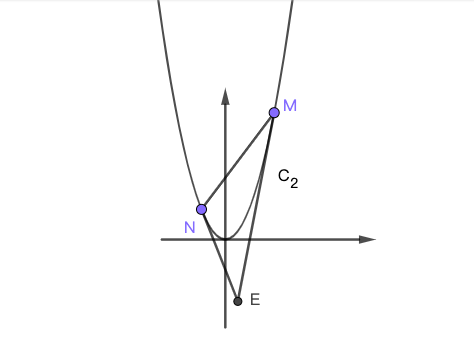
图 9. 第九题(3)
本作品采用创作共用版权协议, 要求署名、非商业用途和保持一致. 转载本站内容必须也遵循署名-非商业用途-保持一致的创作共用协议.

发表回复