实验数据独立性检验小记
检验A,B两组数据的相关性是实验中经常碰到的问题. 在本文中我将以具体例子来说明如何在Excel中做独立性测试, 这里我用的是卡方检验.
卡方做独立性检验举例
Example . 假设A,B两组数据如下(完整的数据可以看文末的xls附件), 教程中只以图形的方式加以说明:
试用卡方检验来说明$A\geq1$与$B\geq1$是否是相关的.
当然, 这里$1$的选取是有相应的实际意义的, 需要根据你的实验做相应的调整. 但是一般都是对照实验, 因此这里$A\geq a$与$B\geq b$中$a$应该等于$b$, 否则不能作为对照.
统计小知识
关于卡方检验的一点小知识.
Remark .我们必须注意, 统计检验相对于反证法. 我们想要说明数据是相关的, 从而在用统计规律作为工具时, 我们反设数据是独立的(作为$H_0$假设).
我们将利用Excel计算卡方统计值$\chi^2$, 并比较它与在给定的显著水平$\alpha$($\alpha$一般取为0.05,0.01, 也可参考专业的数据库, 毕竟各行各业不一样)下的临界值$\chi^2_\alpha$的大小. 如果$\chi^2<\chi_\alpha^2$, 则接受$H_0$假设(此时统计推断的结论是数据是独立的), 否则拒绝$H_0$假设(此时统计推断的结论是数据是相关的).
计算实际频数与理论频数
根据卡方统计量的计算公式:
$$\begin{equation}\label{eq:1}
\chi^2=\sum_{i=1}^r\sum_{j=1}^c\frac{(A_{ij}-E_{ij})^2}{E_{ij}},
\end{equation}$$
这里, $r$为行数, $c$为列数, 而$A_{ij}$为第$i$行$j$列的实际频数, $E_{ij}$为其理论频数.
从公式$\eqref{eq:1}$, 我们知道需要计算上面两组数据的实际频数与理论频数.
实际频数的统计
利用Excel的COUNTIFS函数可以非常方便的统计实际频数.
- 在Excel中按照下图做好表格, 最好保持单元格一致, 即从
H2到K6的范围, 这在后面公式的引用时, 可以方便地和文中对照.

- 在
I4中录入=COUNTIFS($A$1:$A$50,">=1",$B$1:$B$50,">=1")它表示统计$$A列数据(从A1到A50中满足$\geq1$且$B$列数据中满足$\geq1$的数据的个数). - 同样的道理, 在
J4中录入=COUNTIFS($A$1:$A$50,"<1",$B$1:$B$50,">=1");在I5中录入=COUNTIFS($A$1:$A$50,">1",$B$1:$B$50,"<1");在J5中录入=COUNTIFS($A$1:$A$50,"<1",$B$1:$B$50,"<1"). - 为了计算理论频数, 我们首先需要对实际频数的各行以及各列求和: 在
K4中录入=SUM(I4:J4)计算第一行的和; 在K5中录入=SUM(I5:J5)计算第二行的和;在I6中录入=SUM(I4:I5)以计算第一列的和, 在J6中录入=SUM(J4:J5)计算第二列的和. - 在
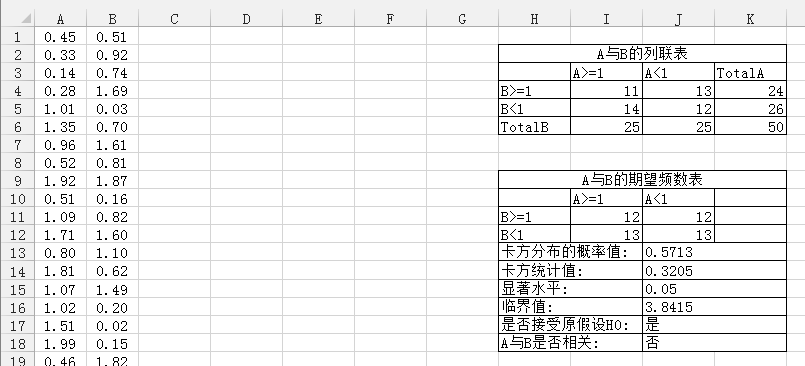
K6中录入=SUM(J4:J5)来计算各行各列数据的和. - 计算结果参考下图, 称为实际频数表或者列联表

理论频数的计算
- 在
I11中录入=I6*K4/$K$6以计算第一行第一列这个单元格的理论频数, 这里规律(or公式)就是计算$(i,j)$(表示$i$行$j$列)位置的理论频数, 我们是将$i$所在行的和乘以$j$所在列的和再除以各行各列的总和. - 同样的道理, 在
J11中录入=J6*K4/$K$6; 在I12中录入=I6*K5/$K$6; 在J12中录入=J6*K5/$K$6. 这样就计算好了理论频数.
卡方统计值的计算
由于Excel直接计算的是卡方统计量所对应的概率值, 因此我们需要先利用CHISQ.TEST计算概率值, 再利用CHISQ.INV计算卡方统计值.
- 在
J13中录入=CHISQ.TEST(I4:J5,I11:J12), 实际上I4:J5就是实际频数的数据块, 而I11:J12就是理论频数的数据块, 公式录入过程中都可以直接用鼠标选择数据块的哈.结果自然是给出卡方统计量的概率值了. (这里稍微有点奇怪(如果你不觉得, 完全可以不看我觉得奇怪的地方, 这毫无影响), 就是Excel可以根据你所选区域而知道自由度, 而公式$\eqref{eq:1}$确不需要自由度就可以计算, 至于为什么Excel要直接计算概率而不直接计算统计量似乎不好理解, 因为从统计量计算相应的概率还需要知道自由度, 这就是我奇怪之处. ) - 计算自由度$\mathrm{df}=(r-1)(c-1)$, 这里行数$r=2$, 列数$c=2$, 故$\mathrm{df}=1$.
- 利用
CHISQ.INV计算相应的统卡方计值:在J14中录入=CHISQ.INV(1-J13,1). 这里J13是概率值, 而1是自由度df. 之所以要用1-J13是因为CHISQ.INV给出的是累计密度下的卡方值. - 在
J15中设置临界水平为$0.05$. - 在
J16中计算在给定的临界水平下相应的临界值:=CHISQ.INV(1-J15,1) - 比较统计值与临界值的大小, 得到是否接受$H_0$假设. 在
J16中录入=IF(J14<J16,"是",否), 即若统计值小于临界值, 则表明在给定的显著水平下, 数据的差异不显著, 从而接受$H_0$; 否则拒绝$H_0$ - 在
J17z中录入=IF(J17="是","否","是")以根据是否接受$H_0$来判断数据是否相关. 即在接受$H_0$时表明数据在给定显著水平下不相关, 而在拒绝$H_0$时表明数据在给定显著水平下相关.
Remark .
- 上面的过程实际上可以推广到多于$2$行$2$列的情形, 没有实质差异.
- 在具体应用时, 若还是两行两列的情形, 则只需利用
COUNTIFS重新计算实际频数, 其他地方会自动计算, 不用更改. - 需要计算不同显著水平, 只需把$0.05$换成其它显著水平即可, 后面的结果会自动改变.
若你还有任何疑问, 欢迎留言讨论.
最终的Excel(2013)文件:下载

发表回复